グレイコードを使ったマルチ制御ゲートなどのメモ

制御ビットが$ n $個ある場合のマルチ制御ゲートを(制御ビットが1個の制御ゲートを使って)構成する方法をまとめる。

制御ビット$ x _ 1,x _ 2,\cdots,x _ n $が$ x _ i=0,1 $の値をとるとき、

$$ \require{physics} \begin{align*} 2^{n-1} x_1 x_2 \cdots x_n =& \sum_{r=1}^n \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < n+1} x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} \\ =& x_1 + \cdots + x_{n} \\ & - x_1 \oplus x_2 - x_1 \oplus x_3 - \cdots - x_{n-1} \oplus x_n \\ & + x_1 \oplus x_2 \oplus x_3 + \cdots x_{n-2} \oplus x_{n-1} \oplus x_n \\ & \cdots \\ & + \qty(-1)^n x_1 \oplus x_2 \oplus \cdots \oplus x_n \end{align*} $$

つまり、制御ビットを少なくとも1つ以上選ぶすべての選択について、 選んだ制御ビットに応じた符号(奇数個なら+、偶数個なら-)をかけて足し合わせると、 全制御ビットのAND(に$ 2 ^ {n-1} $を乗じたもの)になる。 なお、このときの加算および減算は、通常の整数としての加減算。

全制御ビットのANDを$ U $の肩に乗せると、 全制御ビットのANDが成立するときは$ x _ 1 x _ 2 \cdots x _ n=1 $で$ U ^ 1=U $が作用し、 そうでないときは少なくとも1つ$ x _ i=0 $なものがあるので$ x _ 1 x _ 2 \cdots x _ n=0 $となって$ U ^ 0=I $と恒等ゲートが作用するので マルチ制御Uゲート$ U ^ {x _ 1 x _ 2 \cdots x _ n} $が作れる。

これは、

$$ \begin{align*} U^{x_1 x_2 \cdots x_n} &= {\underbrace{\qty(U^{2^{-n+1}})}_{=V}} ^{2^{n-1} x_1 x_2 \cdots x_n} \\ &= V^{2^{n-1} x_1 x_2 \cdots x_n} \\ &= V^{ \sum_{r=1}^n \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < n+1} x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} } \\ &= \prod_{r=1}^n \prod_{0 < l_1 < l_2 < \cdots < l_r < n+1} V^{ \qty(-1)^{r-1}x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} } \\ &= V^{x_1} \cdots V^{x_{n}} V^{- x_1 \oplus x_2} V^{- x_1 \oplus x_3} \cdots V^{- x_{n-1} \oplus x_n} V^{x_1 \oplus x_2 \oplus x_3} \cdots V^{x_{n-2} \oplus x_{n-1} \oplus x_n} \cdots V^{ \qty(-1)^n x_1 \oplus x_2 \oplus \cdots \oplus x_n } \end{align*} $$

となるので、 制御ビットを少なくとも1つ以上選ぶすべての選択について、 選んだビットを制御ビットとして制御ユニタリゲートを作用させる(奇数個なら$ V=U ^ {2 ^ {-n+1}} $、偶数個なら$ V ^ {-1}=V ^ \dagger $)とよい。 XORは単純に制御Xゲートを順に作用させると構成できる。 制御ビットの選択は、nビット二進数の各ビットを各制御ビットに対応させて、 対応するビットが1のときに選択し、0のときに選択しないようにすればOK。 このとき、ハミング距離が1ずつ変わるようにグレイコードの順で数え上げると、 うまい具合にキャンセルが生じるので都合がよい。

帰納法での証明

$$ \begin{align*} 2^{n-1} x_1 x_2 \cdots x_n &= \sum_{r=1}^n \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < n+1} x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} \end{align*} $$

を帰納法で証明する。

n=2のとき

$$ \begin{align*} 2 x_1 x_2 &= x_1 + x_2 - x_1 \oplus x_2 \end{align*} $$

を示せばよい。

$ x _ 1=x _ 2=0 $の場合、両辺とも0になる。 $ x _ 1, x _ 2 $の一方のみが1の場合、 左辺は0、 右辺についても、単一ビットに対応する項のうち1つのみが1で、XORに対応する項も1なので、キャンセルして0になる。 $ x _ 1=x _ 2=1 $の場合、 左辺は2、 右辺についても、単一ビットに対応する項の両方が1で、XORに対応する項は0なので、あわせて2になる。

つまり、$ x _ i=0,1 $の値をとるとき、上記は成立する。

論理式$ A,B $について、真偽値を0,1で表現するときも同様に成立する。

$$ \begin{align*} 2 A B &= A + B - A \oplus B \end{align*} $$

n=kのとき成立するとして、n=k+1のとき

$ n=k $のとき、

$$ \begin{align*} 2^{k-1} x_1 x_2 \cdots x_k &= \sum_{r=1}^k \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < k+1} x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} \end{align*} $$

が成立すると仮定する。

このとき、右辺の各項$ x _ {l _ 1} \oplus x _ {l _ 2} \oplus \cdots \oplus x _ {l _ r} $も0,1いずれかの値を取る論理式なので、 $ x _ {k+1} $とのANDをとって2倍すると、上記$ A,B $についての式と同様にして以下が成立する。

$$ \begin{align*} 2 \underbrace{x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r}}_{A} \cdot \underbrace{x_{k+1}}_{B} &= \underbrace{x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r}}_{A} +\underbrace{x_{k+1}}_{B} -\underbrace{x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r}}_{A} \oplus \underbrace{x_{k+1}}_{B} \end{align*} $$

これを使うと、$ x _ 1 $から$ x _ {k+1} $までANDを取って$ 2 ^ k $倍したものは、 上記の$ n=k $についての式も使って、

$$ \begin{align*} 2^{k} x_1 x_2 \cdots x_k x_{k+1} =& \sum_{r=1}^k \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < k+1} 2 \qty[ x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} ] \cdot x_{k+1} \\ =& \sum_{r=1}^k \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < k+1} \qty[ x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} +x_{k+1} -x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} \oplus x_{k+1} ] \\ =& \sum_{0 < l_1 < k+1} x_{l_1} + \underbrace{ \sum_{r=1}^k \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < k+1} }_{=1} + x_{k+1} & \mbox{(1次の項)} \\ & -\sum_{0 < l_1 < l_2 < k+1} x_{l_1} \oplus x_{l_2} -\sum_{0 < l_1 < k+1} x_{l_1} \oplus x_{k+1} & \mbox{(2次の項)} \\ & +\sum_{0 < l_1 < l_2 < l_3 < k+1} x_{l_1} \oplus x_{l_2} \oplus x_{l_3} +\sum_{0 < l_1 < l_2 < k+1} x_{l_1} \oplus x_{l_2} \oplus x_{k+1} & \mbox{(3次の項)} \\ & + \cdots \\ & +\qty(-1)^{r-1}\sum_{0 < l_1 < \cdots < l_r < k+1} \overbrace{x_{l_1} \oplus \cdots \oplus x_{l_r}}^{\mbox{$r$次}} -\qty(-1)^{r-2}\sum_{0 < l_1 < \cdots < l_{r-1} < k+1} \overbrace{x_{l_1} \oplus \cdots \oplus x_{l_{r-1}}}^{\mbox{$r-1$次}} \oplus x_{k+1} & \mbox{($r$次の項)} \\ & + \cdots \\ & -\qty(-1)^{k-1} x_{l_1} \oplus \cdots \oplus x_{k} \oplus x_{k+1} & \mbox{($k+1$次の項)} \\ =& \sum_{r=1}^{k+1} \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < k+2} x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} \end{align*} $$

ここで、1次の$ x _ {k+1} $の項の係数$ \sum _ {r=1} ^ k \qty(-1) ^ {r-1} \sum _ {0 < l _ 1 < l _ 2 < \cdots < l _ r < k+1} $について、 この総和の各項はk+1ビットの二進数に対応し($ r $は値が1となるビットの数、$ l _ 1,\ldots,l _ r $は値が1となるビットの位に対応)、 000…0に対応する項のみを除いて符号(奇数個なら+、偶数個なら-)をかけた上で総和を取っている。 000…0に対応する項(=-1)まで含めて総和を取ると全部キャンセルして0になるところ、 その項(=-1)のみが除かれているので、結局総和の値は1となる。

結論

このように、$ n=2 $の場合に成立し、 $ n=k $で成立すると仮定すると$ n=k+1 $の場合にも成立するので、 $ n>2 $で以下が成立する。

$$ \begin{align*} 2^{n-1} x_1 x_2 \cdots x_n &= \sum_{r=1}^n \qty(-1)^{r-1} \sum_{0 < l_1 < l_2 < \cdots < l_r < n+1} x_{l_1} \oplus x_{l_2} \oplus \cdots \oplus x_{l_r} \end{align*} $$

例

トフォリゲート

制御制御Xゲートを構成する。 n=2で、$ U=X $の場合に対応。 $ X=HZH $なので、制御制御Zゲートを作って、標的ビットをHで挟めばよい。

制御制御Zゲートは、 $ 2 x_1 x_2= x_1 + x_2 -x_1 x_2$ の関係と $Z^{1/2}=S$ を使って、

$$ \begin{align*} Z^{x_1 x_2} &= S^{2 x_1 x_2} \\ &= S^{x_1 + x_2 -x_1 \oplus x_2} \\ &= S^{x_1} S^{x_2} {S^\dagger}^{x_1 \oplus x_2} \end{align*} $$

と書ける。

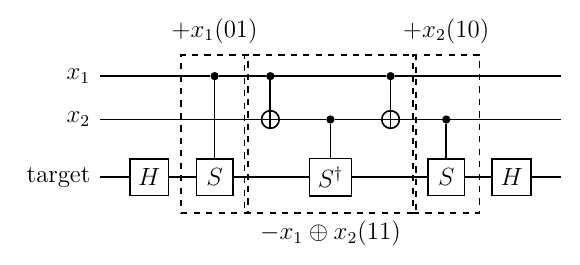
ということで、制御Sゲート $ S ^ {x _ 1}, S ^ {x _ 2}, {S ^ \dagger} ^ {x _ 1 \oplus x _ 2} $を順次作用させればよい。 この各ゲートは、2ビット二進数01,10,11にそれぞれ対応する。 制御ビットの状態を変えず、標的ビットには互いに可換な$ S,S ^ \dagger $が作用するので、 どのような順序で作用させてもよい。 ここでは、 対応する2ビット二進数がグレイコード順になるように(1つずつビット値が変化するように)、 01,11,10の順、すなわち $ S ^ {x _ 1}, {S ^ \dagger} ^ {x _ 1 \oplus x _ 2}, S ^ {x _ 2} $ の順に作用させる。

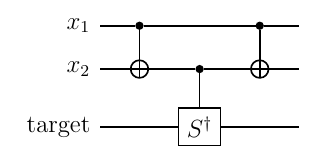
2ビット二進数11に対応する $ {S ^ \dagger} ^ {x _ 1 \oplus x _ 2} $は、 下記のように、

• 最高位ビットを標的ビットとし、1である他のビットを制御ビットとした制御$ X $ゲート
• 最高位ビットを制御ビットとした(単一)制御$ S $ゲート

で実現する。制御ビットの状態を戻すように、制御Sゲートの後にも同様に制御Xゲートを入れる。

以上をまとめると、制御Sゲートを使って、トフォリゲートは次のように書ける。

ところで、制御Sゲートは次のように書ける。

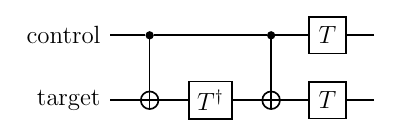
これを代入して、トフォリゲートは次のようにT(およびそのエルミート共役)、H、および制御Xで書ける*1

制御制御制御Uゲート

制御制御制御Uゲートを構成する。 n=3の場合に対応。 $ 4 x_1 x_2 x_3 = x_1 + x_2 + x_3 -x_1 x_2 -x_1 x_3 -x_2 x_3 +x_1 x_2 x_3 $ の関係と $U^{1/4}=V$を使って、

$$ \begin{align*} U^{x_1 x_2 x_3} &= V^{4 x_1 x_2 x_3} \\ &= V^{ x_1 + x_2 + x_3 -x_1 \oplus x_2 -x_1 \oplus x_3 -x_2 \oplus x_3 +x_1 \oplus x_2 \oplus x_3 } \\ &= V^{x_1} V^{x_2} V^{x_3} {V^\dagger}^{x_1 \oplus x_2} {V^\dagger}^{x_1 \oplus x_3} {V^\dagger}^{x_2 \oplus x_3} V^{x_1 \oplus x_2 \oplus x_3} \end{align*} $$

と書ける。

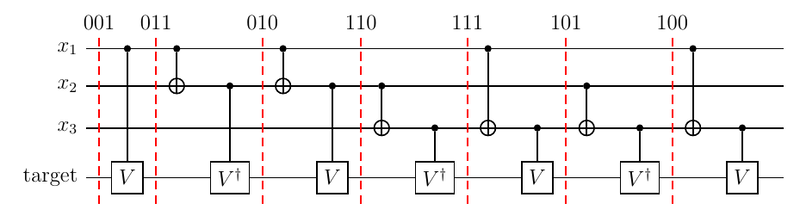
ということで、制御Vゲート $V ^ {x _ 1}, V ^ {x _ 2}, V ^ {x _ 3}, {V ^ \dagger} ^ {x _ 1 \oplus x _ 2}, {V ^ \dagger} ^ {x _ 1 \oplus x _ 3}, {V ^ \dagger} ^ {x _ 2 \oplus x _ 3}, V ^ {x _ 1 \oplus x _ 2 \oplus x _ 3}$ を順次作用させればよい。 この各ゲートは、3ビット二進数001, 010, 100, 011, 101, 110, 111にそれぞれ対応する。 制御ビットの状態を変えず、標的ビットには互いに可換な$ V,V ^ \dagger $が作用するので、 どのような順序で作用させてもよい。 ここでは、 対応する3ビット二進数がグレイコード順になるように、 001,011, 010,110, 111,101, 100 の順、すなわち $ V ^ {x _ 1}, {V ^ \dagger} ^ {x _ 1 \oplus x _ 2}, V ^ {x _ 2}, {V ^ \dagger} ^ {x _ 2 \oplus x _ 3}, V ^ {x _ 1 \oplus x _ 2 \oplus x _ 3}, {V ^ \dagger} ^ {x _ 1 \oplus x _ 3}, V ^ {x _ 3} $ の順に作用させる。

複数ビットが1であるような3ビット二進数110に対応する $ {S ^ \dagger} ^ {x _ 2 \oplus x _ 3} $などは、

• 最高位ビットを標的ビットとし、1である他のビットを制御ビットとした制御$ X $ゲート
• 最高位ビットを制御ビットとした(単一)制御$ V $ゲート

で実現する。制御ビットの状態を戻すように、制御Vゲートの後にも同様に制御Xゲートを入れる。

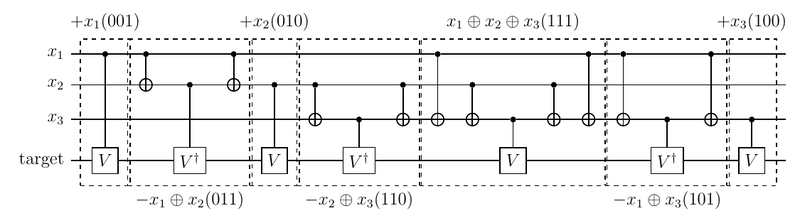
対応する3ビット二進数がグレイコード順になるように各ゲートを作用させているので、 となりあうゲートの間で共通する制御Xゲート（変化していないビットに対応する制御Xゲート）がキャンセルする。 これを使って整理すると下記のようになって、 この記事にあるように機械的に構成できるようになる。

*1:$ TT ^ \dagger=I $としたり、もう少し整理できる